
.....................................................................................................................................................
What Is Escape Velocity?
Akash Peshin
Escape Velocity is the minimum velocity an object must have to
escape a celestial body’s gravitational field permanently, without ever falling
back again.
Contrary to popular wisdom, the moon does have an atmosphere, which is technically
called an exosphere.
It is so incredibly thin and sparse that its particles
seldom collide.
The reason why it’s so thin is that, unlike Earth, the
moon’s gravitational pull is so incredibly weak, that it cannot hold onto the
gases that hover above it or exude from its craggy interior.
The majority of the gas
particles the lunar rocks release dart upwards at a velocity that is greater
than the moon’s escape velocity – the minimum velocity an object must have to
escape a celestial body’s gravitational field permanently, without ever falling
back again.
Escape
Velocity
Now,
because the gravitational strength of a body is a function of its mass, it is
obvious that massive celestial bodies are much harder to escape.
Naturally,
the Earth’s escape velocity is much greater than the moon’s, but much less than
that of Jupiter, which boasts the highest escape velocity among all the
planets, due to its massive size.
One
consequence of the velocity’s dependence on mass is the paradoxical problem we
face while sending a probe to planets more massive than Earth.
The probe
must carry a huge surplus of fuel because the amount of fuel it must combust to
take off and escape that newly explored planet is drastically greater than the
amount it combusted to take off and escape Earth.
However,
when it totes this extra fuel along on the trip, it becomes heavier and
therefore more difficult to accelerate to Earth’s escape velocity.
Escape
velocity equation
An object can escape a
celestial body of mass M only when its
kinetic energy is equal to its gravitational potential energy.
The kinetic energy of an
object of mass m traveling at a
velocity v is given by ½mv².
The gravitational potential
energy of this object, by definition, is a function of its distance r from the center of the celestial body.
This is given by GMm/r, where G is the
Gravitational constant whose value is  .
.
Equating the two, we get: 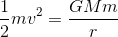
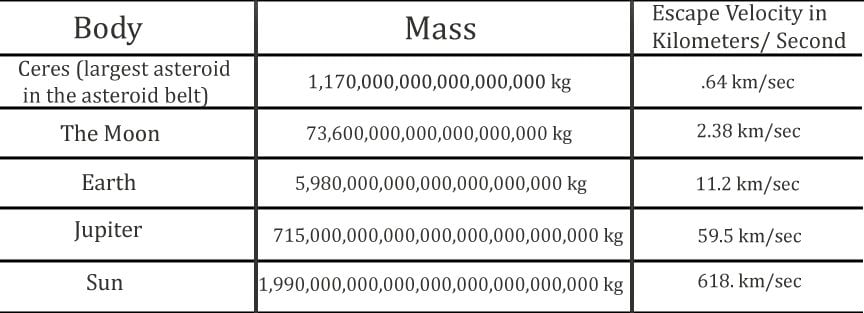
One can substitute
different values of M and r in this equation to determine the escape velocity
of different celestial bodies.
The dependence on r also
implies that objects high above the body’s surface find it easier to escape
than objects resting on it.
This is obvious because the
strength of a planet’s gravitational pull decreases as we move away from its
surface.
Lastly, one can infer from the
equation that a planet’s escape velocity is independent of the object’s mass.
This is counterintuitive, but
whether it is a dinosaur or a turtle, it must travel at 11.2 km/s (neglecting
air resistance) to escape Earth!
Acceleration, however, is a
function of mass, so even though the dinosaur escapes at the same velocity as
the turtle, accelerating it to 11.2 km/s is much more
difficult than accelerating the turtle to the same velocity.
Akash Peshin is
an Electronic Engineer from the University of Mumbai, India and a science
writer at ScienceABC. Enamored with science ever since discovering a picture
book about Saturn at the age of 7, he believes that what fundamentally fuels
this passion is his curiosity and appetite for wonder.

 |
To escape Earth’s gravitational field without
ever falling back again, a rocket must travel at 11.2 km/s.
|
 |
The moon has what is called an exosphere.
|

No comments:
Post a Comment