HYDROSTATIC PRESSURE - Fluid Pressure and Depth – Hydrostatic pressure is the pressure that is exerted by a fluid at equilibrium at a given point within the fluid, due to the force of gravity. Hydrostatic pressure increases in proportion to depth measured from the surface because of the increasing weight of fluid exerting downward force from above. If a fluid is within a container then the depth of an object placed in that fluid can be measured. The deeper the object is placed in the fluid, the more pressure it experiences. This is because the weight of the fluid is above it. The more dense the fluid above it, the more pressure is exerted on the object that is submerged, due to the weight of the fluid.

........................................................................................................

Hydrostatic Pressure

What is Hydrostatic Pressure-- Fluid Pressure and Depth

The air around us at sea level presses down on us at 14.5 pounds per square inch (1 bar).

We do not feel this pressure since the fluids in our body are pushing outward with the same force.

But if you swim down into the ocean just a few feet and you will start to notice a change. You will start to feel an increase of pressure on your eardrums.

This is because of an increase in hydrostatic pressure which is the force per unit area exerted by a liquid on an object.

The deeper you go under the sea, the greater the pressure pushing on you will be.

For every 33 feet (10.06 meters) you go down, the pressure increases by 14.5 psi (1 bar).

Hydrostatic pressure is the pressure that is exerted by a fluid at equilibrium at a given point within the fluid, due to the force of gravity. 

Hydrostatic pressure increases in proportion to depth measured from the surface because of the increasing weight of fluid exerting downward force from above.

If a fluid is within a container then the depth of an object placed in that fluid can be measured.

The deeper the object is placed in the fluid, the more pressure it experiences. This is because the weight of the fluid is above it.

The more dense the fluid above it, the more pressure is exerted on the object that is submerged, due to the weight of the fluid.

Let us derive the formula for Pressure on a object submerged in a fluid:

From, what is pressure: Pressure = Force/Area

From, what is Force: Force = mass x acceleration = m x g (acceleration in gravity)

So: Pressure = F/A = mg/A

From What is Density: Density = Mass/Volume ; Mass= Density x Volume

We now have Pressure = (density x volume x acceleration)/area.

The formula that gives the P pressure on an object submerged in a fluid is therefore: P = r * g * h r (rho) is the density of the fluid, g is the acceleration of gravity h is the height of the fluid above the object

The pressure due to the liquid alone (i.e. the gauge pressure) at a given depth depends only upon the density of the liquid, the acceleration of gravity and the distance below the surface of the liquid.

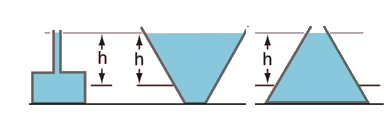
The static fluid pressure at a given depth does not depend upon the total mass, surface area, or the geometry of the container.

P = r * g * h

Pressure = (density of liquid) x (acceleration gravity) x (height)
If the container is open to the atmosphere above, the added atmospheric pressure must be added if one is to find the total pressure on an object.

The pressure at a given depth in a static liquid is a result the weight of the liquid acting on a unit area at that depth plus any pressure acting on the surface of the liquid.

Ptotal = Patmosphere + Pfluid

Ptotal = Patmosphere + ( r * g * h )

Example: 

Find the pressure on a scuba diver who is 10 meters below the surface of the ocean. Assume standard atmospheric conditions. Use the density of sea water = 1.03 X 10³ kg/m³and the atmospheric pressure of 1.01 x 10⁵ N/m ².

Solution:

Pfluid = r g h = (1.03 x10 3 kg/m3) (9.8 m/s²) (10 m) = 1.09 x 10⁵ N/m ².
Ptotal = Patmosphere + Pfluid = (1.01 x 10⁵) + (1.09 x 10⁵) Pa = 2.10 x 10⁵ Pa ( Pascals)

https://www.edinformatics.com/math_science/hydrostatic_pressure.htm