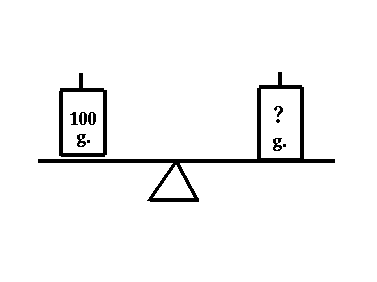
.......................................................................................
Mass And Weight
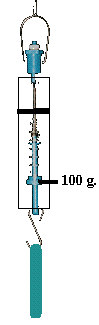
Shown below are
two types of scales commonly used in the classroom -- a spring scale (left) and
a simple balance beam scale on the right.
On earth the
spring scale reads 100g with an unknown mass attached at the bottom. To balance
the scale on the right a 100g mass was also needed.
If we were to
take both scales to the moon, what would the the spring scale read?
How much mass
would be needed to balance the 100g mass on the balance beam? Can you explain
your answer?
 | 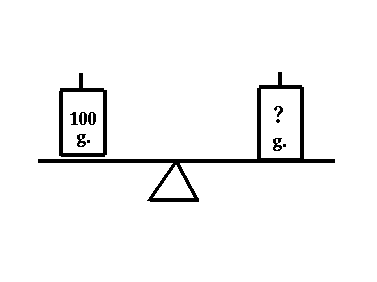 | |
spring scale
|
simple balance scale
|
|
|
||
|
|
grams
The balance scale on the right would need:
grams.
What is the scale on the left really measuring (type one word
and only in lower-case letters?
What did the
above experiment demonstrate?
It shows that
the scale on the left was measuring the force of gravity (weight) not mass.
On earth the
spring was standardized to read 100g at sea level.
A true balance
beam (like a triple beam balance you use at school) measures mass by balancing
the scale against a known (standardized) mass.
On the moon the
mass on the left side of the balance may 'exert less force', but then less
force will be needed to balance it.
So what is
really mass and weight if they are not the same thing?
Mass is
defined as the amount of matter an object has.
One of the
qualities of mass is that it has inertia.
As an example
of inertia, imagine an ice puck resting on a frozen pond. It takes a certain
amount of force to set the puck in motion.
The greater the
mass the more force will be needed to move the puck.
The same is
true if the puck were sliding along the ice. It would continue to slide until a
force is applied to stop the puck.
The more
massive the puck is, the more force will be needed to stop the motion of the
puck. Mass is a measure of how much inertia an object shows.
The weight of
an object on earth depends on the force of attraction (gravity) between the
object object and earth.
We can express
that force as an equation:
F = G[M m/r2]
,
where F is the
force of attraction, M is the mass of the earth, m is the mass of the object,
and r is the distance between the center of mass of the two objects (G is
called the Gravitational Constant)
What does this
equation show? What will cause the force of attraction to increase or decrease?
If either mass
increases the force of attraction increases proportionally. Since the moon has
1/6 the mass of earth, it would exert a force on an object that is 1/6 that on
earth.
Why is
the 1/r 2 factor so important? This is an
inverse square relationship which seems to show up a lot in physics. How does
it affect the force?
What is 1/r 2 when
r=1, 2, 5, 10? What is the decimal equivalent?
Notice that
when r=1 the value 1/r 2 is 1.0, but at r=10
it deceases to 1/100. That means gravity gets weak 'quick' as we move away from
the earth.
To get a real
feel for the inverse square relationship, see if you can get two magnets.
Move the poles
closer and closer slowly, what do you notice when r (the distance between the
poles) is very small?

No comments:
Post a Comment